Définition
\(\triangleright\) Définition du champ électrostatique crée par une charge ponctuelle
Le champ \(\vec E\) crée en \(M\) par un charge ponctuelle en \(P\)
$$\vec E={{\frac{q}{4\pi\epsilon_0r^2}\vec e_r}}\qquad \vec e_r=\frac{\vec {PM} }{PM}$$
Avec:- \(\vec E\): le champ électrostatique en \(V.M^{-1}\)
\(\triangleright\) Définition du champ électrostatique créé par une distribution de charges
- Pour une distribution de \(N\) charges ponctuelles \(q_i\):
$$\vec E={{\sum_{i=1}^N\vec E_i}}$$- Pour une distribution de charges continue dans l'espace:
$$\vec E={{\iiint d^{(3)}\vec E}}$$
Caractéristiques
Le champ électrostatique est un
Champ conservatif et un
champ irrotationnel
Champ créé par une charge ponctuelle
Grâce à l'équation du champ électrostatique \(\vec E=\frac{q\vec u_r}{4\pi\epsilon_0r^2}\), on peut tracer les lignes de champ
On observe:
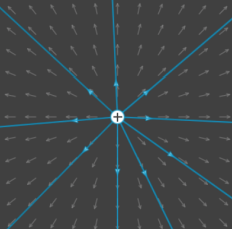
Champ créé par un doublet
Considérons deux charges ponctuelles de signe opposé. C'est ce qu'on appelle un doublet électrostatique.
Les lignes de champ partent de la charge positive à la négative:
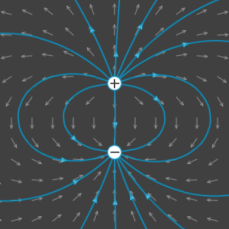
On observe ici un plan de symétrie et un plan d'antisymétrie (en raison du signe opposé)
Champ crée par deux charges de même signe
Considérons deux charges de même signe et de valeur différente situé sur un axe horizontal.
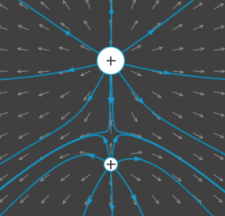
Les lignes partent également des charges positives.
Un plan de symétrie est également présent mais pas de plan d'antisymétrie.
On observe également un point ou le champ est nul appelé
point singulier
Remarque
Si \(q_A\lt 0\), le champ \(\vec E_A\) est centripète
Si \(q_A\gt 0\), le champ \(\vec E_A\) est centrifuge
Plus on s'éloigne, plus \(\vec E_A\) est petit
La plus petite charge possible est \(1,6\times 10^{-19}\;\mathrm C\)
\(1\;\mathrm C\) est une charge énorme
Dans un milieu diélectrique
Le champ électrique se comporte différemment dans les
Milieux diélectriques
On s'intéressent uniquement, ici, aux champs macroscopiques pour l'étude des milieux.
\(\triangleright\) Définition du champ électrique macroscopique
Le champ électrique macroscopique est la moyenne des champs microscopique:
$$\vec E(M)={{\frac 1\tau \iiint_{B(M,R)}\vec E_{microscopique}(P)d\tau(P)}}$$
Avec:- \(B(M,R)\): une boule de rayon \(R\)
Approximation dipolaire


